Month: December 2015

The graphviz visualisations we’ve been using for quipu have quite a few limitations, as they tend to make very large images, and there is limited control over how they are drawn. It would be better to be able to have more of an overview of the data, also rendering the knots in the right positions with the pendants being the right length.

Meet the pixelquipu!

These are drawn using a python script which reads the Harvard Quipu Database spreadsheet file and renders quipu structure using the correct colours. The knots are shown as a single pixel attached to the pendant, with a colour code of red as single knot, green for a long knot and blue as a figure of eight knot (yellow is unknown or missing). The value of the knot sets the brightness of the pixel. The colour variations for the pendants are working, but no difference between twisted and alternating colours, also no twist direction is visualised yet.

Another advantage of this form of rendering is that we can draw data entropy within the quipu in order to provide a different view of how the data is structured, as a attempt to uncover hidden complexity. This is done hierarchically so a pendant’s entropy is that of it’s data plus all it’s sub-pendants, which seemed most appropriate given the non-linear form that the data takes.

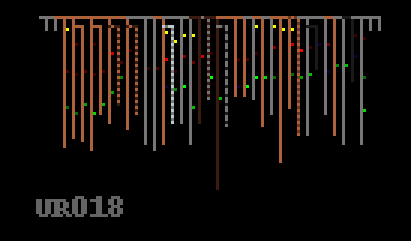
We can now look at some quipus in more detail – what was the purpose of the red and grey striped pendants in the quipu below? They contain no knots, are they markers of some kind? This also seems to be a quipu where the knots do not follow the decimal coding pattern that we understand, they are mostly long knots of various values.

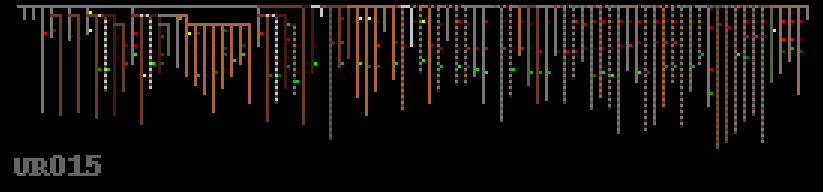
There also seems to be data stored in different kinds of structure in the same quipu – the collection of sub-pendants below in the left side presumably group data in a more hierarchical manner than the right side, which seems much more linear – and also a colour change emphasises this.

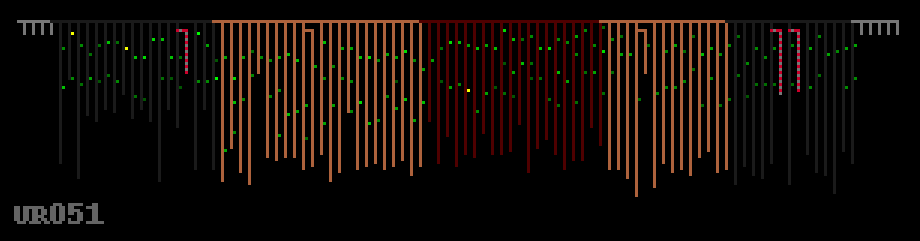
Read left to right, this long quipu below seems very much like you’d expect binary data to look – some kind of header information or preamble, followed by a repeating structure with local variation. The twelve groups of eight grey pendants seem redundant – were these meant to be filled in later? Did they represent something important without containing any knots? We will probably never know.

The original thinking of the pixelquipu was to attempt to fit all the quipus on a single page for viewing, as it represents them with the absolute minimum pixels required. Here are both pendant colour and entropy shown for all 247 quipu we have the data for:

Archaeologists can read a woven artifact created thousands of years ago, and from its structure determine the actions performed in the right order by the weaver who created it. They can then recreate the weaving, following in their ancestor’s ‘footsteps’ exactly.

This is possible because a woven artifact encodes time digitally, weft by weft. In most other forms of human endeavor, reverse engineering is still possible (e.g. in a car or a cake) but instructions are not encoded in the object’s fundamental structure – they need to be inferred by experiment or indirect means. Similarly, a text does not quite represent its writing process in a time encoded manner, but the end result. Interestingly, one possible self describing artifact could be a musical performance.

Looked at this way, any woven pattern can be seen as a digital record of movement performed by the weaver. We can create the pattern with a notation that describes this series of actions (a handweaver following a lift plan), or move in the other direction like the archaeologist, recording a given notation from an existing weave.

A weaving and its executable code equivalent.

One of the potentials of weaving I’m most interested in is being able to demonstrate fundamentals of software in threads – partly to make the physical nature of computation self evident, but also as a way of designing new ways of learning and understanding what computers are.

If we take the code required to make the pattern in the weaving above:

(twist 3 4 5 14 15 16)
(weave-forward 3)
(twist 4 15)
(weave-forward 1)
(twist 4 8 11 15)

(repeat 2
 (weave-back 4)
 (twist 8 11)
 (weave-forward 2)
 (twist 9 10)
 (weave-forward 2)
 (twist 9 10)
 (weave-back 2)
 (twist 9 10)
 (weave-back 2)
 (twist 8 11)
 (weave-forward 4))

We can “compile” it into a binary form which describes each instruction – the exact process for this is irrelevant, but here it is anyway – an 8 bit encoding, packing instructions and data together:

8bit instruction encoding:

Action  Direction  Count/Tablet ID (5 bit number)
0 1         2              3 4 5 6 7 

Action types
weave:    01 (1)
rotate:   10 (2)
twist:    11 (3)

Direction
forward: 0
backward: 1

If we compile the code notation above with this binary system, we can then read the binary as a series of tablet weaving card flip rotations (I’m using 20 tablets, so we can fit in two instructions per weft):

0 1 6 7 10 11 15
0 1 5 7 10 11 14 15 16
0 1 4 5 6 7 10 11 13
1 6 7 10 11 15
0 1 5 7 11 17
0 1 5 10 11 14
0 1 4 6 7 10 11 14 15 16 17
0 1 2 3 4 5 6 7 11 12 15
0 1 4 10 11 14 16
1 6 10 11 14 17
0 1 4 6 11 16
0 1 4 7 10 11 14 16
1 2 6 10 11 14 17
0 1 4 6 11 12 16
0 1 4 7 10 11 14 16
1 5

If we actually try weaving this (by advancing two turns forward/backward at a time) we get this mess:

The point is that (assuming we’ve made no mistakes) this weave represents *exactly* the same information as the pattern does – you could extract the program from the messy encoded weave, follow it and recreate the original pattern exactly.

The messy pattern represents both an executable, as well as a compressed form of the weave – taking up less space than the original pattern, but looking a lot worse. Possibly this is a clue too, as it contains a higher density of information – higher entropy, and therefore closer to randomness than the pattern.